AutoDiff

http://www.columbia.edu/~ahd2125/post/2015/12/5/

https://pytorch.org/docs/stable/_modules/torch/autograd.html#grad

https://alexey.radul.name/ideas/2013/introduction-to-automatic-differentiation/

https://rufflewind.com/2016-12-30/reverse-mode-automatic-differentiation

 

Cat or Dog

Stats -> ML -> AI

Image Retrieval Using Deep Learning

RMAC RESNET

We propose a novel approach for instance-level image retrieval. It produces a global and compact fixed-length representation for each image by aggregating many region-wise descriptors. In contrast to previous works employing pre-trained deep networks as a black box to produce features, our method leverages a deep architecture trained for the specific task of image retrieval. Our contribution is twofold: (i) we leverage a ranking framework to learn convolution and projection weights that are used to build the region features; and (ii) we employ a region proposal network to learn which regions should be pooled to form the final global descriptor. We show that using clean training data is key to the success of our approach. To that aim, we use a large scale but noisy landmark dataset and develop an automatic cleaning approach. The proposed architecture produces a global image representation in a single forward pass. Our approach significantly outperforms previous approaches based on global descriptors on standard datasets. It even surpasses most prior works based on costly local descriptor indexing and spatial verification1

Click to access 1604.01325.pdf

https://arxiv.org/abs/1511.05879

https://arxiv.org/abs/1510.07493

https://arxiv.org/abs/1610.07940

https://github.com/figitaki/deep-retrieval

https://www.kaggle.com/c/landmark-retrieval-challenge/discussion/57855#335578

Deep image retrieval learning global representations for image search from Universitat Politècnica de Catalunya

RL

 

• http://karpathy.github.io/2016/05/31/rl/
• https://deepmind.com/blog/reinforcement-learning-unsupervised-auxiliary-tasks/
• https://arxiv.org/abs/1705.05363

 

RateMyView

Visual Vocabulary

Designing with data

There are so many ways to visualize data – how do we know which one to pick? Use the categories across the top to decide which data relationship is most important in your story, then look at the different types of chart within the category to form some initial ideas about what might work best. This list is not meant to be exhaustive, nor a wizard, but is a useful starting point for making informative and meaningful data visualizations.

 

https://github.com/ft-interactive/chart-doctor/tree/master/visual-vocabulary

Kaggle Vanity

https://www.kaggle.com/vincento/competitions

Blade Runner Principle

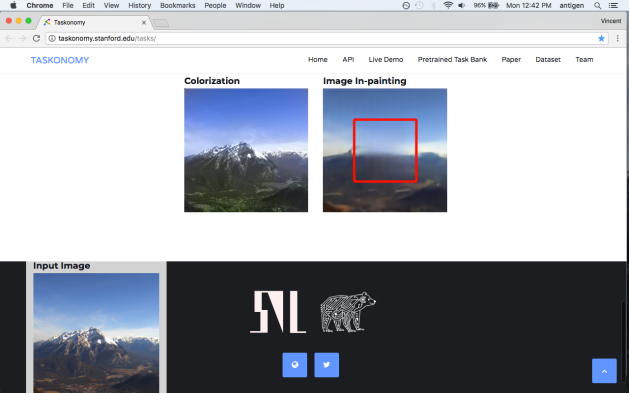
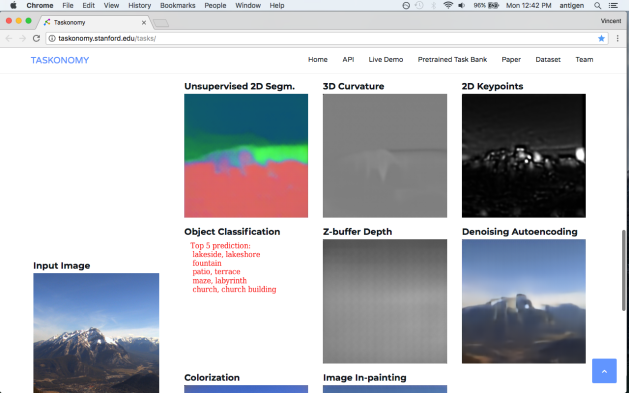
Malware  < ————————————————————————— > Detector

Generator  < ————————————————————————- > Discriminator

One network generates candidates and the other evaluates them. Typically, the generative network learns to map from a latent space to a particular data distribution of interest (benignware), while the discriminative network discriminates between instances from the true data distribution and candidates produced by the generator. The generative network’s training objective is to increase the error rate of the discriminative network (i.e., “fool” the discriminator network by producing novel synthesized instances that appear to have come from the true data distribution).

 

Adversarial stuff

https://arxiv.org/abs/1712.09665

Click to access 1511.07528.pdf

Click to access 1605.07277.pdf

https://www.usenix.org/conference/usenixsecurity16/technical-sessions/presentation/tramer

Click to access 1708.06733.pdf

Click to access privacy-igert.pdf

Click to access af4067d0b51794c3ae91fccfd1909d784a5b.pdf

Click to access 1709.00440.pdf

Click to access 1610.06918v1.pdf

https://www.darpa.mil/program/cyber-grand-challenge

https://machine-learning-and-security.github.io/

http://www.ai-sec.net/AISec2017/index.html

https://nips.cc/Conferences/2017/Videos

http://www.secrepo.com/